 Note added 1 March 2017: The Cozzone shape factor for common cross sections is now in the Section Properties of Common Cross Sections spreadsheet. There are expressions for many more cross sections. This subject is covered in depth in the new edition of our free textbook. This post can be considered obsolete.
Note added 1 March 2017: The Cozzone shape factor for common cross sections is now in the Section Properties of Common Cross Sections spreadsheet. There are expressions for many more cross sections. This subject is covered in depth in the new edition of our free textbook. This post can be considered obsolete.
In writing the plastic bending section for our (soon to be released) free textbook I started to look into the origin of the shape factor for the cross section of a beam for plastic bending. It is explained in Bruhn and in other references but in the past I have always just used the existing section shape factors without making the to find out what they really were.
It is no secret (it is defined in most of the references) that the shape factor ‘k’ is equal to the plastic section modulus divided by the elastic section modulus – so it is an expression of the plastic bending capacity over the elastic bending capacity.
The elastic bending modulus is easily found – there are many references and methods available to calculate the elastic modulus (2nd moment of area divided by the distance to the outer fiber or I/c). The plastic bending modulus is less simple and less easily available.
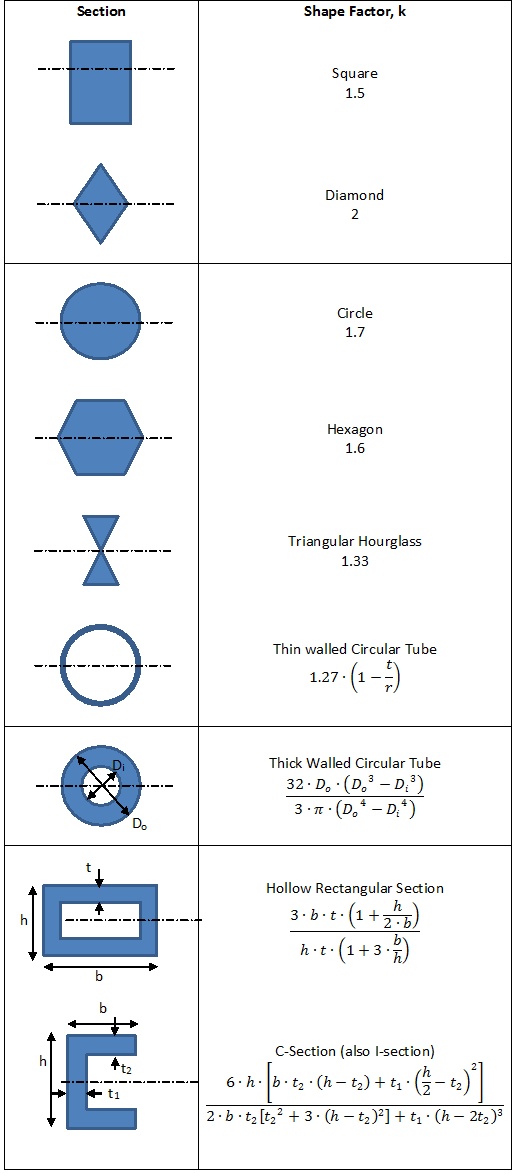
In the figure to the left, I have collected the traditional, and some additional expressions, for the cozzone shape factor.
We have also produced a spreadsheet that will calculate the cozzone shape factor for a symmetrical section of compound rectangular shapes. Make sure to read the note at the top of the spreadsheet and always sanity check the result.
If anyone out there knows a better general method for the calculation of section plastic modulus I would love to hear from you.
Happy Stressing!
To try our free Stress Analysis Engineering Spreadsheets click below
To try our Add-in for Microsoft Excel for Windows click below




The information provided for shape factor of thick wall cylinder and hollow rectangular cross sections are wrong. Plz do correct it.
Hey Sunil – I have added a further note to the top of the post that the table is obsolete and the correct spreadsheet and textbook 2nd edition should be consulted.
For a thick walled circular tube, the factor in the numerator should be 16 and not 32. Using the 32 factor gives a shape factor much greater than the 1.7 value for a solid circular section, which should not be possible.
Sunil is correct and the spreadsheet doesn’t seem to address circular sections. For a thick walled circular tube, the factor in the numerator should be 16 and not 32. Using the 32 factor gives a shape factor much greater than the 1.7 value for a solid circular section, which should not be possible.
Kevin, there is a note at the top of the page that referes the reader to https://www.abbottaerospace.com/downloads/aa-sm-001-000/ – this has the correct derivation and also includes a wider range of shapes