The Neuber method for plasticity is based on the idea that the stress levels produced by finite element models that use a linear material model, in some circumstances, when they exceed the proportional limit, or yield stress, will be conservative and unrealistic.
This method is applicable to the stresses caused by stress concentrations created by geometric features and for the method to be applicable the following must be true:
- The finite element mesh should be fine enough to accurately predict the actual peak stress at the features.
- The material should be ductile enough to allow for local redistribution.
- There must be enough local material at a lower stress level to allow for local redistribution.
- The stress field should be largely linear, or uniaxial in nature.
The strain energy at the peak elastic stress should be calculated. The strain energy is the area under the linear stress-strain curve:
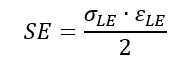
The intercept where the line of constant strain energy crosses the elasto-plastic stress-strain curve is taken to be the corrected plastic stress/strain state that will occur in the actual material, such that:
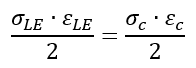
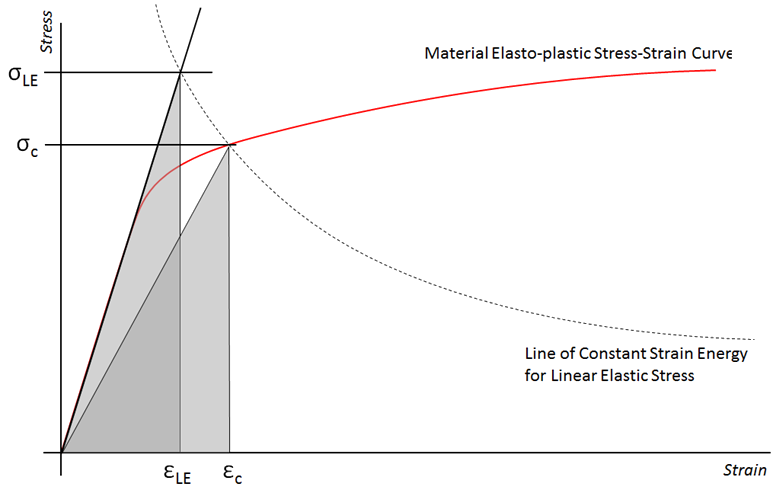
It can be seen that the actual area under the elasto-plastic stress-strain curve is greater than the triangle given by the Neuber stress level and so this method is potentially conservative.
A spreadsheet of this analysis method is given at the link below:
