The simplest approach for column strength that is generally applicable to long, elastic columns with stable cross sections is the Euler method:
The Euler long strut formula:
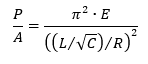
Where:
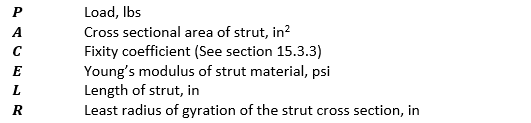
The term (L/R) is called the slenderness ratio, or S, and the effective slenderness ratio is the slenderness ratio modified by the fixity coefficient in the following way: (L/√C)/R, this gives the basic term for the squared denominator of the Euler equation.
Plotting the Euler column allowable is for a given material stiffness over a range of effective slenderness ratio values gives the following result.
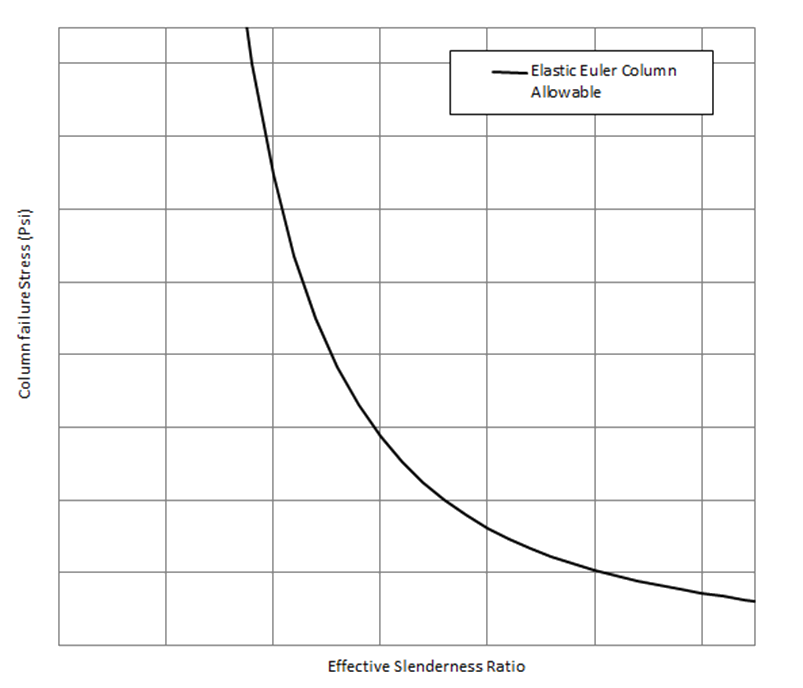
Note that as the effective slenderness ratio reduces the strength of the column increases at an increasing rate. At low effective slenderness ratios the Euler approach gives unrealistic results as the allowable stress exceeds the elastic limit of the material.
The Euler allowable can also exceed the ultimate strength of the material. The spreadsheet method includes a ‘cap’ to the Euler allowable of Ftu, however in reality it is almost certain that the column will fail at some stress value below Ftu:
